 NEUTRON
NEUTRON
 Help
Help
Bilbao Crystallographic Server
 NEUTRON NEUTRON
 Help Help
|
NEUTRON is a computer program for calculating the phonon extinction rules for inelastic neutron scattering experiments. Given the space group and the phonon symmetry specified by the wave vector q, the program examines the inelastic neutron scattering activity of the corresponding phonons for all possible types of scattering vectors Q=H-q, where H is a reciprocal lattice vector.
The applied algorithm is based on a recently proven theorem that demonstrates the existence of symmetry-based selection rules for the phonon activity in inelastic neutron scattering experiments: the resulting phonon absences depend only on the mode symmetry and the scattering vector Q, and not on the specific atomic positions of the crystal structures (Perez-Mato et al., 1998). Using the distribution of the reciprocal lattice vectors (Brillouin zones) into types with respect to the symmetry group of the scattering vector, it is possible to show that Brillouin zones belonging to the same type are characterized by the same set of selection rules. The derived extinction rules prove to be very useful for the identification of the symmetries of the measured phonons, and their systematic use helps the optimization of inelastic neutron scattering experiments (Aroyo et al., 2002a). These selection rules also apply to phonon X-ray inelastic scattering, and their use has been successfully extended to thermal diffuse scattering studies (Aroyo et al., 2002b).
For more details related to the program NEUTRON, its algorithm and the procedure for the calculation of the phonon selection rules, the user is referred to Kirov et al., 2003.
REFERENCES
Space-group specification:
Option 1: Enter the sequential numbers of the supergroup G and subgroup H as given in International Tables for Crystallography volA (referred to as ITA) or choose them from the table of space groups. Please note the default choices of the space-group settings which are used in this program.
Option 2: It is also possible to carry out the calculations for a non-default setting of the space group. In this case the user is expected to provide the transformation between the user-chosen coordinate system of the space group and that of the default ITA-setting. The transformation consists of a rotational (3x3) matrix and an origin shift (3x1) column.
q-vector data: NEUTRON expects q-vector coefficients in the form of 3 decimal numbers and a label of the wave-vector. The q-vectors are neither restricted to the representation domains nor to the Brillouin zones. The program accepts q-vector coefficients determined with respect to different coordinate systems of the reciprocal space:
Table 1: Conventional q-vector coefficients (q1, q2,q3) expressed by the primitive q-vector
coefficients (qp1,qp2,qp3)
|
Lattice types |
q1 |
q2 |
q3 |
|---|---|---|---|
|
aP, mP, oP, tP, cP, rP, hP |
qp1 |
qp2 |
qp3 |
|
mA, oA |
qp1 |
qp2-qp3 |
qp2+qp3 |
|
mC, oC |
qp1+qp2 |
-qp1+qp2 |
qp3 |
|
oF, cF |
-qp1+qp2+qp3 |
qp1-qp2+qp3 |
qp1+qp2-qp3 |
|
oI, cI, tI |
qp2+qp3 |
qp1+qp3 |
qp1+qp2 |
|
hR |
qp1-qp2 |
qp2-qp3 |
qp1+qp2+qp3 |
Option 3: There is also a possibility to input the wave-vector coordinates referred to a coordinate system which is dual to the non-default setting of the space group defined by the user (see Option 2 in Space-group specification)
The OUTPUT of the program consists of three main blocks: a Space-group data block, a q-vector data block including the little group irreducible representations (irreps), and a data-block with Q-vector types and extinction rules.
The listed data starts with the ITA number of the space group and its lattice type. Then follows the set of non-translation generators used by the program for the construction of the matrix-column pairs of the coset representatives of the group with respect to its translation subgroup. Both the generators and the coset representatives are listed in a (3x4) matrix form.
The wave-vector block starts with the information on the q-vector coordinates given by the user. For the calculations the program uses conventional dual wave-vector coordinates, i.e. those referred to a coordinate system of the reciprocal space which is dual to the default conventional settings of the space group. The translational coset representatives of the little group of the wave vector are listed as matrix-column pairs in a (3x4) matrix form. The matrices of the little group representations are listed for all translational coset representatives of the little group in a consecutive order. The matrix coefficients (in general complex) are given in the polar form (modulus and phase angle [deg]. The labels of the representations consist of the wave-vector letter(s) and a consecutive number determined by the order of the irrep generation.
A line with the conventional dual coordinates of the general form of the scattering vector Q = H-q = (h-q1, k-q2, l-q3) indicates the beginning of the block. The extinction rules are listed in subblocks corresponding to the different types of Q-vectors. These types are distinguished by the different sets of restrictions on the values of the components h,k,l of the lattice vector H(h,k,l). The strict point group of a Q-vector type consists of all those elements of the little co-group which leave the Q-vector invariant. The phonon extinction rules are checked for pnonon symmetries, i.e. for all irreps of the little group. A symmetry type (irrep) of phonons can be active in inelastic neutron scattering experiments if it is listed as 'Allowed'.
Example 1: Phonon extinction rules for q=(0,0,0) with label GM, for the space group Pnma
INPUT: Specification of the space-group and the wave-vector data:
This is the look and feel of the input form of the program NEUTRON. The user must enter the ITA number of Pnma which is 62, and the q-vector coordinates (0,0,0), and its label: GM.
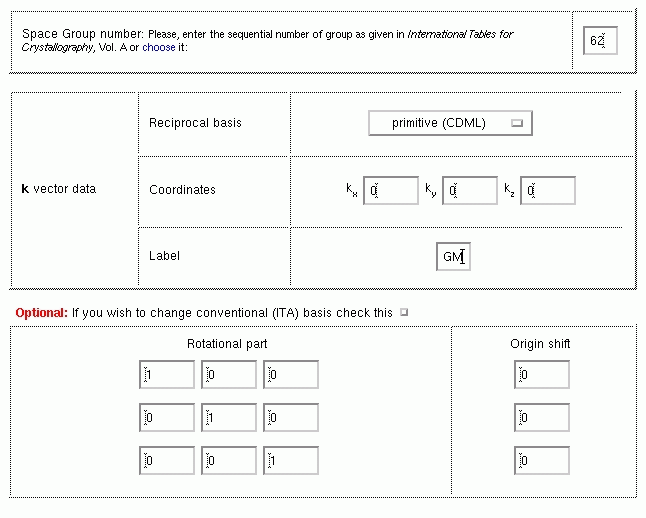
OUTPUT: To see the results for the extinctions the space group Pnma, q=(0,0,0), click here.
The space-group data-block of the OUTPUT contains the list of the non-translational generators as chosen in ITA. For example, in the case of Pnma this set is <(2z|1/2,0,1/2),(2y|0,1/2,0),(-1|0,0,0)> (shown in the form of (3x4) matrices). The sets of 8 translational coset representatives for the group corresponds to the 'general position' lists of ITA. The wave-vector data-block starts with the q-vector coordinates followed by a list of the translational coset reprsentatives of the little group. As the wave vector we are considering is GM, its little group coincides with the space group Pnma and the 8 little group irreps for both cases are simply related to the irreps of the point group mmm.
The results listed in the data-block on the Q-vector types start with the general form of the scattering vector Q=H-q, which in this case coincides with the reciprocal lattice vector H. There are 7 special (nontrivial) Q-vector types, represented by the corresponding Brillouin zone vectors H. The strict point groups refer to the representives of the scattering-vector types which are listed. For example, the strict point group of H(0,0,l) is 2mm = {1, 2z, my, mx }. The extinctions rules are given in blocks for each scattering vector type. Due to the non-symmorphic character of Pnma, one gets a different set of selection rules depending on the parity of the values of the h, k,l, components of H. For example, in the case of the Brillouin zone H(0,0,l), the phonons of symmetry GM5 and GM8 can be INS active if l=2n, while for l=2n+1, the active irreps are GM1 and GM4.
|
Bilbao
Crystallographic Server http://www.cryst.ehu.es |
For comments, please mail to cryst@wm.lc.ehu.es |